Calculus Notes
⟵Section 1.1 Section 1.3 ⟶Section 1.2: Finding Limits Graphically and Numerically
Limits
If a function $f(x)$ approaches a particular value $L$ when $x$ gets arbitrarily close to a particular number $c$, the function is said to have a limit at $c$ equal to $L$. Mathematically, this statement is written $$\lim_{x\to c} f(x) = L$$ For example, consider the function $f(x) = 2x$. Here, calculating limits is straightforward. One can see that as $x$ gets arbitrarily close to 3, the function $f(x)$ gets arbitrarily close to 6, i.e. $$\lim_{x\to c} 2 x = 6 $$ It is not necessary for the function to actually exist at the point where the limit is evaluated. For example, the function $$f(x) = \frac{x^3-1}{x-1}$$ does not exist when $x = 1$, because $f(1)$ results in a division by zero. However, the limit of $f(x)$ as $x$ approaches 1 does exist and is equal to 3. We can see this by plugging in values of $x$ that are successively closer to 1:
| $x$ | 0.75 | 0.9 | 0.99 | 0.999 |
| $f(x)$ | 2.313 | 2.710 | 2.970 | 2.997 |
| $x$ | 1.25 | 1.1 | 1.01 | 1.001 |
| $f(x)$ | 3.813 | 3.310 | 3.030 | 3.003 |
Nonexistant limits
The function $f(x) = \frac{|x|}{x}$ does not have a limit at $x=0$, because the function does not approach a particular value. Instead, as $x$ approaches 0 from the left, $f(x)$ approaches -1, while as $x$ approaches 0 from the right, $f(x)$ approaches 1 (see Figure 1).
Although the limit of this function at $x=0$ does not exist, it can still be said to have the following one-sided limits:
$$\lim_{x \to 0-} \frac{|x|}{x} = -1 \hspace{15pt} \text{and} \hspace{15pt} \lim_{x \to 0+} \frac{|x|}{x} = 1$$If the left-hand and right-hand limits of a function both exist at a point and are equal to each other, then the limit of the overall function at that point exists and has that same value.

Another limit that does not exist is $\displaystyle\lim_{x\to 0} \frac{1}{x^2}$. In this case, the function does not approach any particular value near $x=0$, but instead becomes arbitrarily large for small values of $x$:
$$\lim_{x \to 0} \frac{1}{x^2} = \infty$$Formal definition of limits
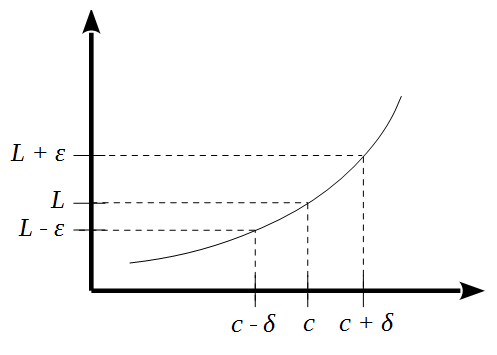
Consider again the limit $$\lim_{x\to c} f(x) = L$$ Let us suppose that $c$ varies by a small amount $\delta$ and the corresponding $L$ value varies by a corresponding amount $\epsilon$ as shown in Figure 2. For the limit to exist, you must be able to make $\epsilon$ as small as you want simply by decreasing the size of $\delta$.